3-3 召回模块：海量候选的快速匹配

在第二节我们简单讲了一下现在推荐系统的目标。假设我们拥有无穷的算力的情况下，采取这种方式计算出来的结果一定是最优的模型推荐效果。

但是现实是，我们不可能拥有无穷的算力。

如果你是第一次了解推荐系统，我先来简单解释下。以新闻推荐为例，推荐系统的目标是从千万甚至更多的新闻候选集中，挑选出用户最可能感兴趣的k篇新闻。(下文为了论述简单，我会默认k=10)。而整个过程，需要在非常短的时间，比如1s内，完成全部的计算。大家可以想象一下下拉刷新时候的那个等待时间，如果这个时间太长，用户肯定不愿意等下去。

出于平衡效果和延迟的原因，现在的推荐系统大多把它划分为召回和排序两个阶段。

• 召回是从候选集中找到用户可能会感兴趣的过程，目的是把千万甚至更多的候选集，变成千级别的候选。
• 排序是接受用户召回的千级别的候选再排序，从中用户最可能感兴趣的10篇新闻。

所以，召回阶段面临的问题是，怎样可以快速从海量内容中找到用户最感兴趣的Top k的候选。

有一些经典的推荐系统的算法，比如协同过滤，包括用户协同过滤(和你相似爱好的人也看过什么)和文章维度的协同过滤(看过你看过的文章的人还看过什么)，这些算法也是可以用在召回阶段的。这些算法在横空出世的时候也是名噪一时无人能出其右。但是现在，这些算法在实际应用的问题中或多或少的会面临一些问题，比如用户协同过滤容易把人都相似到一些全局最活跃的用户上，而文章协同过滤则没有考虑到当前用户的喜好。所以已经渐渐地被业界淘汰了。

目前在召回阶段基本都是通过向量化召回找到用户最感兴趣的内容。而这个向量怎么训练和得到呢？我们来从经典的FM召回谈起。

从FM谈起

对于不熟悉FM这个算法的同学，我强烈建议你们补补课。这是推荐系统近十年来可以说最为划时代意义的一种方法。后面你会发现，所谓深度学习的一套算法，只不过是在FM基础上做了一些搭积木的工作。

谈起FM(Factorization Machine)，如果要从理论上追根溯源的话，有点类似于LR(Logistic Regression)。

在推荐和广告领域，预估的目标是二分类问题(用户是否点击)，特征基本都是网络上的属性特征——离散值比较多，而连续值比较少。在这种场景下使用LR做预估，通常的做法是要把离散特征变成一个个虚拟变量，然后进行逻辑回归。

写成数学形式是这个样子的

$\hat{y_i}(x)=w_0+\sum_iw_i*x_i$

在这种数学表达形式下，各个特征都是独立考虑的，并没有考虑到特征之间的相互关系。但实际上，特征之间是有可能有相互关联的，比如男性用户一般会比较喜欢游戏，而女性用户一般会喜欢时尚。为了建模这种相关性，可以在模型中引入二阶项

$\hat{y_i}(x)=w_0+\sum_iw_i*x_i+\sum_{i,j}w_{ij}x_ix_j$

但这种加入二阶项的方式有一个问题，原始的特征比较稀疏，比如有一个女性用户喜欢Dota2，这种样本可能会在原始数据集中非常少见，会导致二阶项$w_{ij}$学习的非常不准确。

为了解决这个问题，FM引入了一个类似矩阵分解的思路，给每一个类别变量引入了一个向量$v$，把上述式子变成了这个样子

$\hat{y_i}(x)=w_0+\sum_iw_i*x_i+\sum_{i<j} \langle v_i, v_j \rangle x_ix_j$

这样做为什么可以有效呢？

我们来想一下这个v的更新，还是女性用户和Dota2的例子，女性用户的所有样本可以更新$v_{female}$，而Dota2的样本可以更新$v_{dota2}$，这样即使在样本稀少的时候，只要女性和Dota2的样本分布够多，理论上$\langle v_{female}, v_{dota2} \rangle$ 也可以生成正确的预估结果。

至于v向量维度选择的数学依据，其实矩阵分解有关，我们这里就不提了。如果对此有疑问的同学，可以参考文末的参考文献来学习。在实际的应用中，v的维度大多数情况下是一个实验出来的超参数。

FM在推荐系统中的应用

推荐系统中，最主要的问题其实是user和item的匹配问题。而最能体现每一个用户或者物品独一无二性的，其实是用户侧的user_id，和物品的item_id。如果一个推荐系统能够很好的学习到user_id和item_id，那么这个推荐系统一定是非常准确且稳定的。

所以我们来看一个最简单的FM模型：只有user_id和item_id的模型。我们可以把user_id和item_id套入上面的FM公式，可以得到这样一个变换：

$\hat{y_i}(x)=w_0+\sum_{u_i \in user}w_{u_i}*x_{u_i}+\sum_{i_j \in item}w_{i_j}*x_{i_j}+\sum_{u_i \in user}\sum_{i_j \in item} \langle v_{u_i}, v_{i_j} \rangle x_{u_i}x_{i_j}$

回到我们的召回场景。问题本质上是，当user给定的时候，找到系统中得分最高的item。所以上式中的几项实际上可以拆分为

• 给定user与排序无关的项 $w_0$, $\sum_{u_i \in user}w_{u_i}*x_{u_i}$
• 真正决定item顺序的项 $\sum_{i_j \in item}w_{i_j}*x_{i_j}$ 和 $\sum_{u_i \in user}\sum_{i_j \in item} \langle v_{u_i}, v_{i_j} \rangle x_{u_i}x_{i_j}$

当$v_{u_i}$给定时，把bias项$w_{i_j}$合并入向量极端。最终决定每一个item的排序结果会变成一个向量的内积：

$\langle (v_{u_i}, 1), (v_{i_j}, w_{i_j}) \rangle$

所以一个FM模型的训练结果的召回问题，就转化成为一个内积运算找Top k的问题。而内积运算，可以很轻易的转化为cos距离。这个问题就更加进一步的转化为，给定一个user向量，找和它距离最近的Top k的item，也就是我们熟知的kNN问题。

这里顺带说一句，FFM召回作为FM召回的变体，和FM召回实际上是相通的。

向量化召回

在把向量化召回的问题转化为kNN的问题之后，其实我们已经把这个问题解了80%，剩下的就是看怎么样优雅的解决这个kNN问题。

当然kNN这个问题不仅局限于推荐的召回场景。更一般的场景是，比如在搜索中，针对给定的query，怎么从海量候选中找到和这个query最相关的候选结果。

kNN是一种实践和理论结合的典型问题：实际应用中有需要(解决大量候选的召回问题)，于是可以把这个问题抽象成一个具体的数学问题。然后设定benchmark，学术界和工业界一起不断迭代优化，成为一个具体的研究方向。

具体这个问题的数学形式可以定义为以下的样子：

• 给定N个维度是f的向量(vector)组成集合S
• 给定一个距离函数d，其中 d(a, b) 是向量a和b的距离，距离越小表示a，b越相似
• 输入一个维度是f的向量q，如何找到S中和q距离最近的K个向量

首先暴力计算肯是不行的。暴力计算就是维护一个大小为k的堆，然后遍历所有的候选，这样的时间复杂度是O(Nlog(k))。当N非常大，比如千万级别的候选，显然查询是非常慢的。

常见的kNN的优化算法有以下几种：

1. kd-tree: 这是最经典的kNN的查询算法。基于坐标轴进行二叉树分叉，这样可以快速的把所有候选划分到不同的超矩形中。进行查找时，根据二叉树快速找到的二叉树子节点。但是当向量维度比较高时，这种算法一般效果比较差。
2. ball-tree: 实际上是kd-tree的一种改进。不再局限于坐标轴的分叉，沿着一系列的hyper-spheres来分割数据，空间中可以用球来表示。每一个子节点中有一个代表中心的节点，以及一簇候选。进行查找时，先比较目标向量与众多划分出来的球型结构的中心节点的距离，找到最近的中心节点，然后再在这个球型结构的候选中找最近的k个候选。
3. HNSW: 先说NSW，先把候选根据距离构建成一个图，构建时距离最近的点被连成了边。进行查找时，先随机选择初始位置，然后沿着边即可递归的找到所有的最相近的候选；HNSW是在NSW的基础上，加入了层级信息，类似于引入了索引，加快了搜索的速度，以及落入奇怪连通分支的概率。

囿于篇幅，我们不展开说这几种相似算法具体的实现细节了。感兴趣的同学可以在文末的参考文献找到这几种方法的原始论文，看下实现细节。

不过需要注意的一点是，不管这三种的哪一种方法，都是需要离线计算的——不管是kd-tree的方形结构，还是ball-tree的球形结构，抑或者是HNSW的层级结构，都需要先在离线准备好这样一个结构；才可以实现在线的快速计算。

这其中有两个问题：

• FM模型的更新怎样可以联动这个召回的离线结构的更新
• 构建离线结构的速度不能过慢，需要让FM模型的更新可以及时的反馈到这个离线结构上

具体在实现中哪个效果好，还是要结合自己的数据和实验效果，进行取舍；同时还要方便测试和迭代，不同的应用场景肯定效果是不同的，没法一概而论。

双塔召回

上文我们着重讲了FM模型到向量化召回的由来。现在都是深度学习时代了，有没有可能在召回侧加一些深度学习的网络呢？

需要注意的一点是，除了我们要训练出一个各项指标优秀的模型之外，我们还需要尽可能的保留转化为向量化召回的操作空间，否则等待我们的就是百万候选集上的暴力计算。所以，一般意义上的Wide & Deep肯定是不行的。

所以，目前业界的一个比较通用的解决方案是: user侧接一个塔，item侧接一个塔，然后两个tower的顶部，把两个tower的结果做点积。这样就是一个，接了深度网络(保证效果)，同时在user侧和group侧分开计算(保证可以进行kNN运算)的召回模型了。

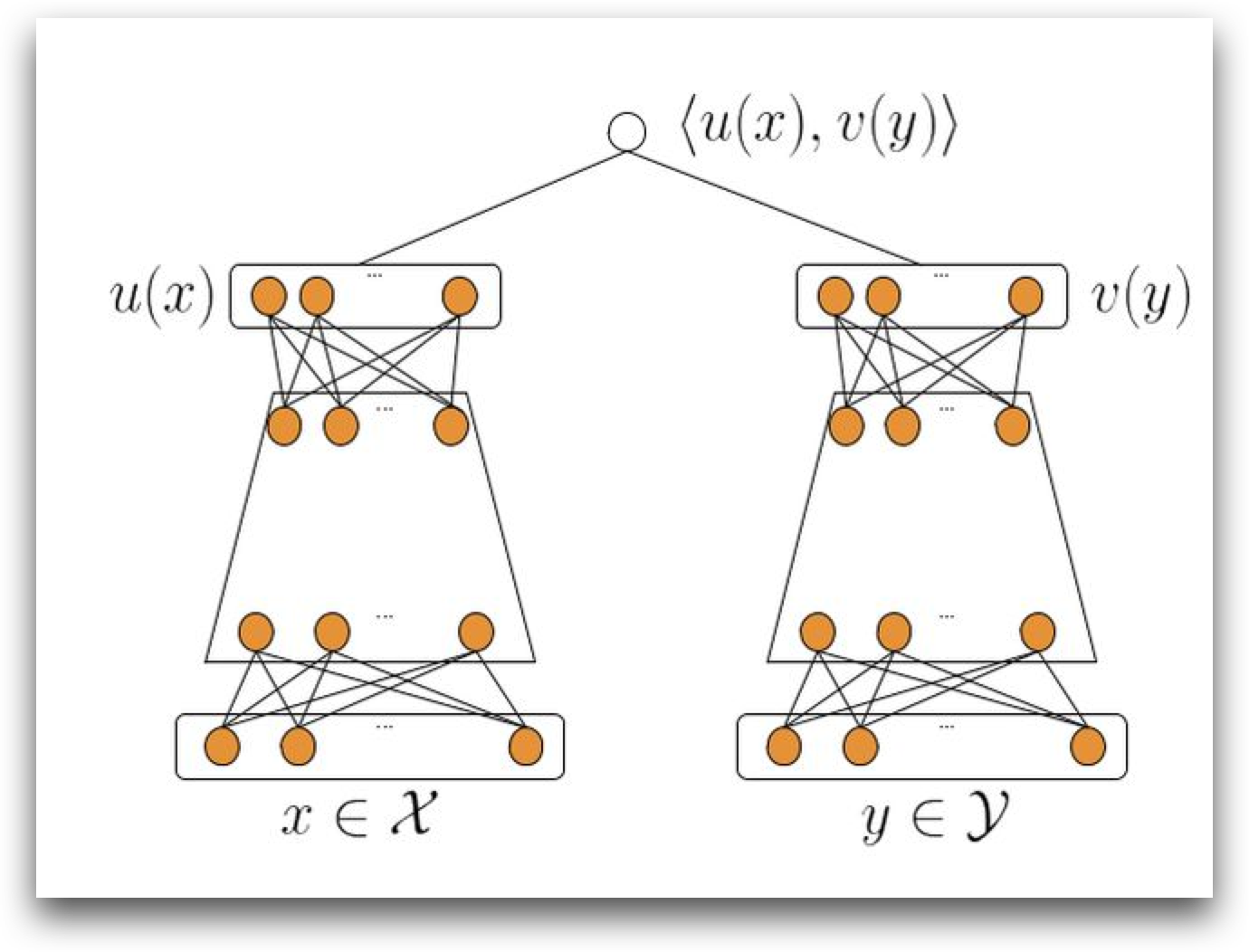
比如YouTube的这篇经典的论文，这边有好多特征其实都是user侧的feature，实际上是user侧的tower。group侧的特征在这张图里都没有出现。

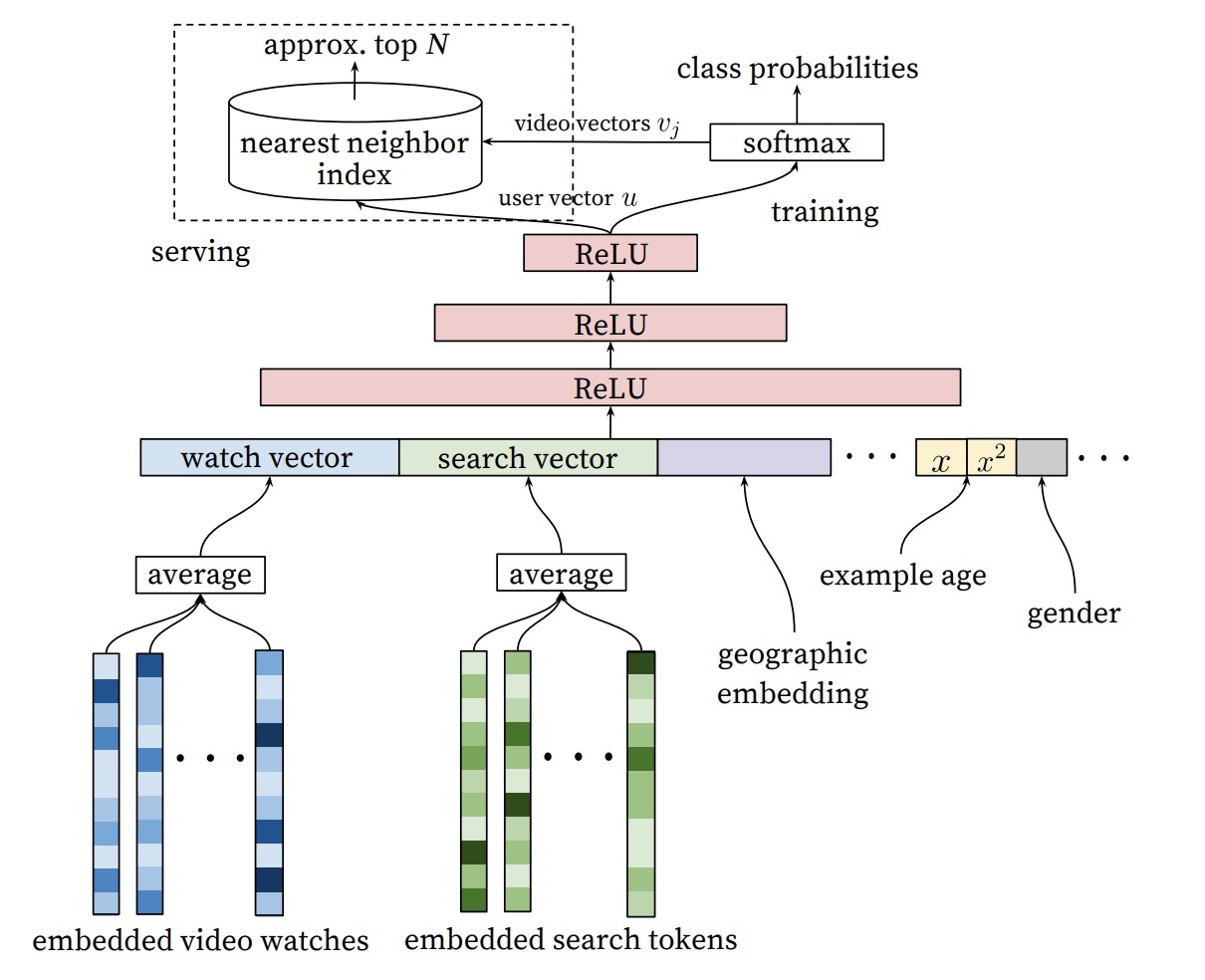
当模型变成双塔后，进行向量化召回的item侧塔的knn结构构建的时候，就不再是以item_id对应的embedding做构建了，而是需要把每一个item的特征的原始值收集起来，先一起forward得到item侧最终要和user侧进行点积的embedding。然后再用这个embedding进行kNN相似结构的构建。

同样，user侧需要最终执行kNN相似计算的，只是user侧最终的embedding，这意味着user侧也可以在召回运算进行之前进行一些预计算，得到最终的user_embedding。这样召回侧的实际计算，依然也就变成了user_embedding * item_embedding的经典kNN问题了。

召回阶段的一些其他问题

在YouTube的论文中，召回问题被看成了一个多分类问题。这篇论文中对于召回问题的解法，类似word2vec。在损失函数换成了多分类的softmax之后，为了解决计算效率问题，采用了随机负采样和层次softmax来优化。这种解法更像是一个nlp领域的解法，并且softmax生成的embedding的用法与FM生成的embedding的用法基本类似。这里就不在具体的说明了。

本文讲述的只是FM召回的演化过程。实际应用中，除了这种召回可能还会有其他类型的召回，比如通过item2vec根据文章的相似性来找回，整体的思路与本文伦论述的FM召回大同小异。

参考文献

• YouTube论文: https://static.googleusercontent.com/media/research.google.com/zh-CN//pubs/archive/45530.pdf
• FM论文: https://cseweb.ucsd.edu/classes/fa17/cse291-b/reading/Rendle2010FM.pdf
• ball-tree: https://arxiv.org/pdf/1511.00628.pdf
• hnsw: https://arxiv.org/pdf/1603.09320.pdf

最后总结一下这篇文章。这文章中我们讲了基础的FM模型，以及如何从FM模型发展成为一个向量化召回问题，最终深度化变成双塔召回模型。